Solveur IA de trigonométrie sur Math.now — outil gratuit en ligne

Résolvez rapidement vos problèmes de trigonométrie grâce à l’IA — gratuit, simple et avec des explications pas à pas sur Math.now.

Salut ! Je suis ton assistant IA sur Math.now. Besoin d’aide en trigonométrie ?

Qu’est-ce que la trigonométrie ?

Introduction à la trigonométrie

La trigonométrie est une branche des mathématiques qui étudie les relations entre les côtés et les angles des triangles. On l’utilise dans de nombreux domaines concrets, comme la construction de ponts ou la navigation maritime.

Notions clés de la trigonométrie

Les notions de base incluent les fonctions sinus, cosinus et tangente, qui relient les angles aux rapports de longueurs dans les triangles rectangles. Il existe aussi des identités, comme celles liées au théorème de Pythagore, et des lois pour les triangles non rectangles. La trigonométrie s’appuie sur la géométrie et sur des outils tels que le cercle trigonométrique.

Comment comprendre la trigonométrie ?

Pensez à la trigonométrie comme à la science qui permet de mesurer les ombres : si un arbre projette une ombre de 10 pieds (≈ 3,05 m) sous un certain angle du soleil, la trigonométrie permet d'en déduire la hauteur sans grimper. Exemples simples : utiliser la tangente pour calculer la pente d’un toit ou le sinus pour modéliser des ondes en musique.

Points forts du solveur IA de trigonométrie sur Math.now

Accès gratuit et immédiat en ligne

Accédez gratuitement au solveur IA de trigonométrie de Math.now — des réponses précises et instantanées, sans inscription.

Interface claire et intuitive

Naviguez dans le solveur via une interface claire et intuitive sur Math.now. Des contrôles simples et un affichage épuré rendent l’outil accessible aux débutants comme aux experts, pour une expérience fluide.

Guidage pas à pas

Des explications détaillées, des étapes guidées et des questions de suivi : le solveur fait office de tuteur IA et propose des astuces interactives pour mieux comprendre.

Utilisable sur tous vos appareils, sans installation

Accessible depuis téléphone, tablette ou ordinateur, sans installation. Gratuit et en ligne, il s’adapte parfaitement à tous les écrans. Profitez d’une expérience homogène sur tous vos appareils pour une aide en trigonométrie à tout moment.

Saisies variées et prise en charge de nombreux types de problèmes

Le solveur IA de problèmes de trigonométrie accepte le texte et les images pour traiter tous les sujets liés à la trigonométrie. En ligne, il vous permet de résoudre rapidement et facilement une large variété de problèmes.

Grande précision pour des résultats rapides et fiables

Obtenez des résultats précis pour gagner du temps et réduire les erreurs. Propulsé par MathGPT, le solveur fournit des réponses fiables qui renforcent vos bases en mathématiques. Cette qualité transforme des problèmes complexes en solutions simples et rapides, tant pour les étudiants que pour les professionnels.

Comment utiliser le Solveur IA de trigonométrie sur Math.now ?

Étape 1 : accédez à Math.now et saisissez votre problème

Rendez-vous sur Math.now et ouvrez l’outil Solveur IA de trigonométrie. Saisissez votre question de trigonométrie ou importez une image de l’énoncé.

Étape 2 : laissez l’IA analyser, puis examinez la solution pas à pas

Une fois soumis, il analyse votre saisie et affiche instantanément des solutions pas à pas.

Étape 3 : copiez et partagez les résultats

Après vérification, copiez la solution en un clic pour la conserver dans vos notes ou la partager.

Exemples de problèmes de trigonométrie résolus sur Math.now

Triangle rectangle simple

Saisissez, par exemple, les côtés 3 et 4 d’un triangle rectangle : le Solveur IA de trigonométrie calcule l’hypoténuse (5) grâce au théorème de Pythagore, puis détermine les angles à partir des rapports de sinus et cosinus. Chaque étape est expliquée clairement pour vous faire gagner du temps sur vos exercices.

Démonstration d’identités

Saisissez sin²θ + cos²θ et demandez de vérifier que l’expression vaut 1. Le Solveur IA de trigonométrie décompose l’expression en s’appuyant sur le théorème de Pythagore et des exemples du cercle trigonométrique, en expliquant les substitutions et les simplifications pour confirmer l’identité pour tout θ.

Exercices pratiques

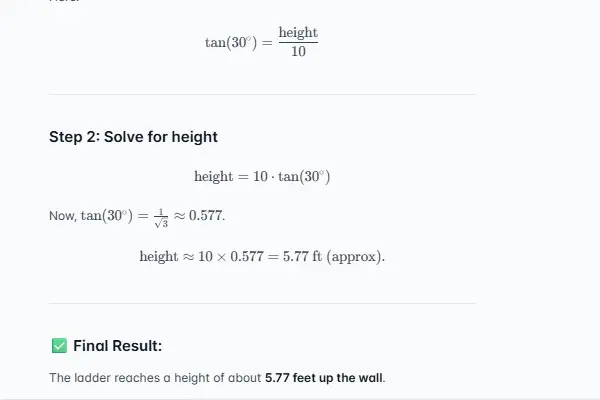
Une échelle est appuyée contre un mur, formant un angle de 30°, la base étant à 10 pieds (≈ 3,05 m) du mur. Le solveur utilise la tangente (opposé/adjacent = tan(30°)) : la hauteur vaut 10 × tan(30°) = 10/√3 ≈ 5,77 pieds (≈ 1,76 m).

Cas d'usage populaires du solveur IA de trigonométrie sur Math.now

Pour les étudiants qui utilisent le solveur IA de trigonométrie en ligne pour leurs devoirs

Les lycéens et étudiants se retrouvent souvent face à des devoirs de trigonométrie difficiles, parfois tard le soir. Avec ce solveur IA de trigonométrie en temps réel, il suffit d’entrer un problème de trigonométrie pour obtenir une réponse immédiate, avec des explications étape par étape et des exemples. Sur Math.now, l’aide aux devoirs est interactive, gratuite et accessible à tout moment. Pour aller plus loin en géométrie, découvrez le solveur de géométrie. Les outils de Math.now ne se contentent pas de donner des réponses : ils renforcent vos compétences et favorisent une compréhension durable.

Pour les pros — le solveur IA de trigonométrie gratuit pour vos projets

Les ingénieurs et concepteurs ont besoin de calculs d’angles rapides dans des projets concrets, comme la conception de ponts ou les simulations physiques. Le solveur IA de trigonométrie traite des cas pratiques, comme l’application du cosinus aux vecteurs de force. En tant que solveur IA de trigonométrie étape par étape, il décompose les équations complexes en étapes claires, assurant précision et efficacité, même sous des délais serrés.

Pour les enseignants — un assistant pédagogique IA en classe

Les enseignants cherchent des méthodes interactives pour expliquer la trigonométrie en classe. Le solveur IA de trigonométrie fait office d’assistant pédagogique : il permet d’illustrer des solutions en direct, de créer des exemples personnalisés (par exemple des démonstrations d’identités) et de générer des séries d’exercices variés. Au final : des explications pas à pas, prêtes à l’emploi, pour aider les élèves à mieux comprendre, sans préparation supplémentaire.